Mathematicians Find Proof to 122-Year-Old Triangle-to-Square Puzzle
A long-standing shape mystery has finally been solved

Illustration of shape shifting polygons.
About a decade ago Tonan Kamata, now a mathematician at the Japan Advanced Institute of Science and Technology (JAIST), stood mesmerized in front of a math museum’s origamilike exhibit. It featured a triangular tile cut into four pieces that were connected by tiny hinges. With a simple swivel, the pieces spun around to transform the triangle into a square.
The exhibit traces its origin to a mathematical puzzle published in a 1902 newspaper. Henry Dudeney, a self-taught English mathematician and puzzle columnist, asked his readers to dissect an equilateral triangle into the smallest number of pieces that could be rearranged into a square. In his next column two weeks later, he noted that a “Mr. C. W. McElroy of Manchester”—Charles William McElroy, a clerk who frequently wrote to Dudeney with puzzle solutions—had a four-piece solution. After two more weeks, Dudeney reported that none of the newspaper’s other readers had bested the solution, and since then, the record has stood. It remained unproven, however, whether a solution with fewer pieces existed.
On supporting science journalism
If you’re enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
The puzzle became known as “Dudeney’s dissection” or the “haberdasher’s problem,” and it was even featured in Scientific American’s June 1958 issue. Martin Gardner, a mathematician and longtime columnist for the magazine, wrote about the quandary.
[Try out Scientific American’s math puzzles]
Now, more than 122 years after it was first proposed, Kamata and two other mathematicians have finally proved that a solution with fewer pieces is impossible. Their result was posted to the server arXiv.org in a December 2024 preprint entitled “Dudeney’s Dissection Is Optimal.”
“I believe many who appreciate mathematics would agree that the simpler an unsolved problem appears, the more profoundly captivating it becomes to those who love mathematics,” Kamata says.
Together with Massachusetts Institute of Technology mathematician Erik Demaine and JAIST mathematician Ryuhei Uehara, Kamata had been developing a new approach to tackle origami-folding problems using graph theory. In graph theory, a graph is essentially a collection of lines, or edges, and vertices, the points where edges meet. The edges and vertices of one graph can be compared with those of another to explore deeper relationships between the two structures—an approach that Kamata thought might help to resolve Dudeney’s dissection.
One part of the problem is fairly simple: a two-piece solution can be ruled out by thinking about the problem’s constraints. For starters, the triangle and square must have equal areas because the pieces are the same. For a square, its longest possible cut is across the diagonal. A bit of pen-and-paper math shows that, unfortunately, the diagonal’s length is too short for the edge of its equal-area triangle, which rules out a two-piece solution.
Proving that there are no three-piece solutions is much trickier, however, and that’s the reason for the century-long delay. Although it is a simple three-piece puzzle, there are an infinite number of ways to cut up the triangle, Demaine says. “Each of those pieces could have arbitrarily many edges to it, and the coordinates of those cuts start at arbitrary points,” he says. “You have these continuous parameters where there’s lots and lots of infinities of possible choices that makes it so annoyingly hard. You can’t just brute-force it with a computer.”
To tackle the problem, the group categorized possible dissections of an equilateral triangle based on how the cuts intersect the triangle’s edges. First, the researchers sorted the infinity of ways to cut the triangle into five unique classifications. They then repeated the exercise for a square and found 38 distinct classifications.
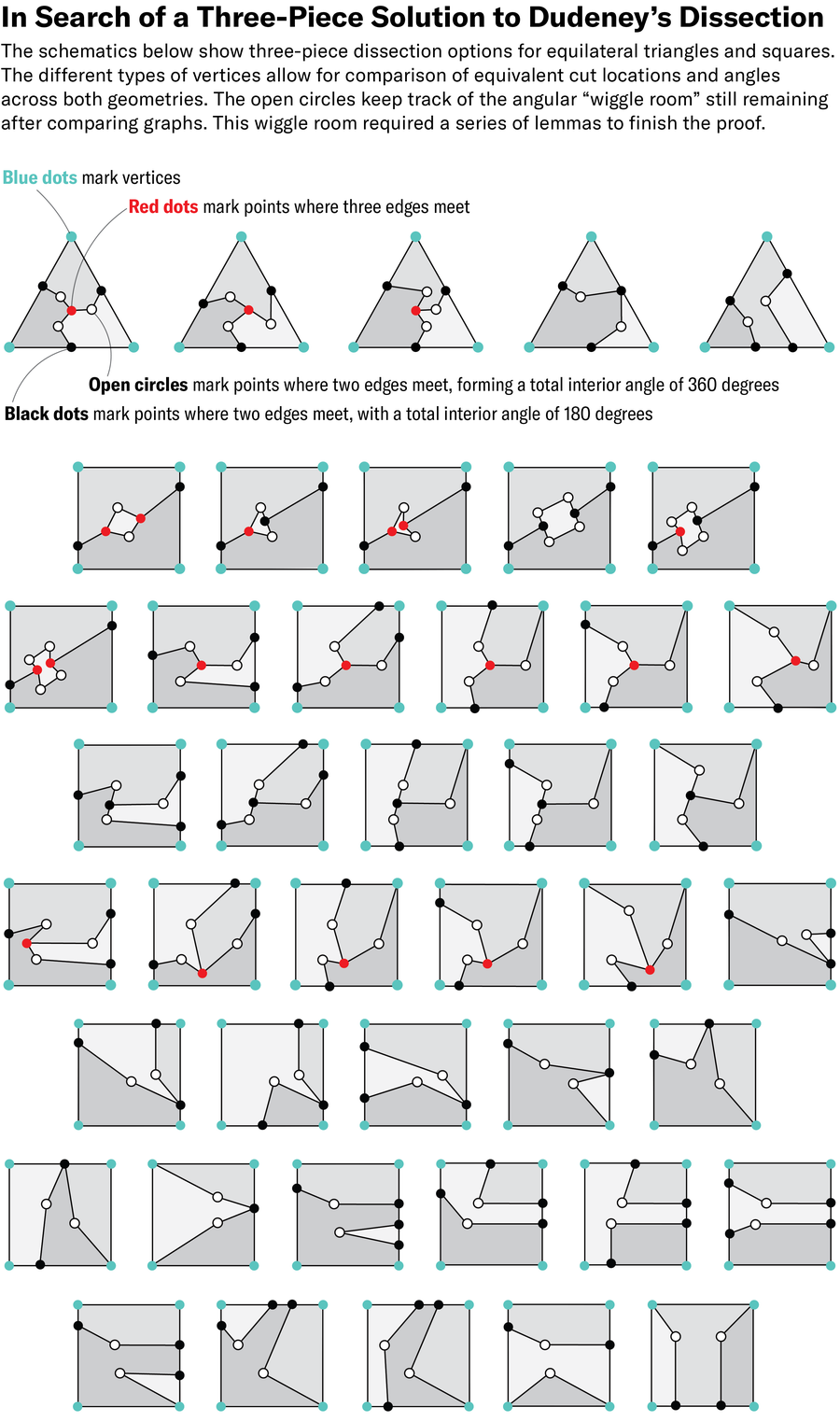
Next, the researchers tried to match a triangular graph to a square one by tracing all the possible paths in each shape and comparing the resulting collections of edge lengths and angles. If one of the squares’ paths had matched that of a triangle’s, it would have meant that the researchers had discovered a three-piece solution.
The approach transformed the continuous problem into a discrete one—almost. Within each classification, there are “still infinitely many places all these vertices could go,” Demaine says. In the end, the group derived a collection of complex lemmas, or intermediate steps in a theorem, that, together with the categories, used proof by contradiction to find no matching paths.
Smith College computer scientist Joseph O’Rourke, who has wrestled with the puzzle on and off for decades and was not involved with the current work, thinks the group’s proof can probably be simplified. He notes that it took a messy collection of highly specific lemmas to eliminate all the possibilities, “Many other researchers would have given up.”.
Crucially, if the authors can simplify their proof, the matching-diagrams technique could unravel a slew of related origamilike open questions. “These problems remind us how much there is yet to discover,” Kamata says. “Anyone can become a pioneer in this frontier.”

